要点：
- KNN（K-Nearist Neighbors）
- 线性分类器：SVM，Softmax
- 双层神经网络
- 图像特征
计算机得到的是像素矩阵
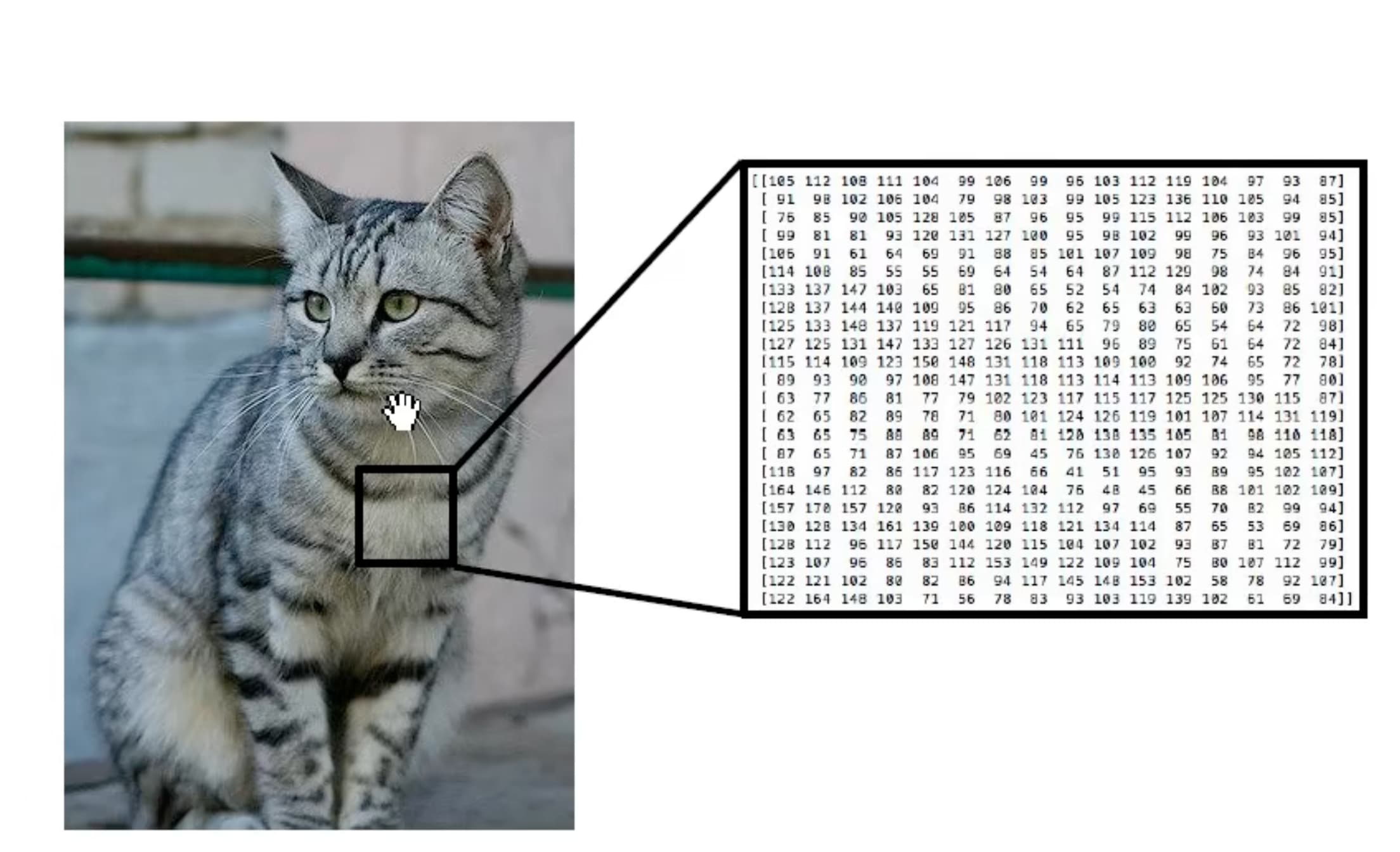
对于计算机辨别分类的难点：
（以猫为例）：
- 拍摄时的光线、角度
- 猫的不同姿态形状
- 猫的不同品种以及数量
- 截取的部分不同以及同框事物的隐藏与遮挡
图像分类相当于一个黑箱”
def classify_image(image):
#some magic here?
return class_label
仿生结构_猫大脑皮层
不同的大脑皮层对视觉不同特征关联，例如边缘、端点、变化或色彩。
~~以提取边缘为例，如果我们将猫的边缘提取然后用算法去识别效率非常的低下。对于每个标签都需要编写一个对应的算法，而且每换一个标签都需要重新去审视和思考并事无巨细地描绘标签事物
BUT ！我们用数据驱动（data-driven approach）的方法 收集带有图像和标签的数据集，采用机器学习训练分类器，并用其测试新的图像。
模式如下：
def train(iamges,labels):
# machine learning!
return model
def predict(model,test_images):
# use moel to predict labels
return test_labels
数据集：CIFAR10
- 10种分类
- 50000训练图像
- 10000测试图像
在训练集中找出若干张与测试集中最相近的的图像
Question：那么如何衡量相似程度？
$L_1$ $d_1 (I_1,I_2)=\sum\limits_{p} |I_1^p-I_2^p|$
各像素差值之和
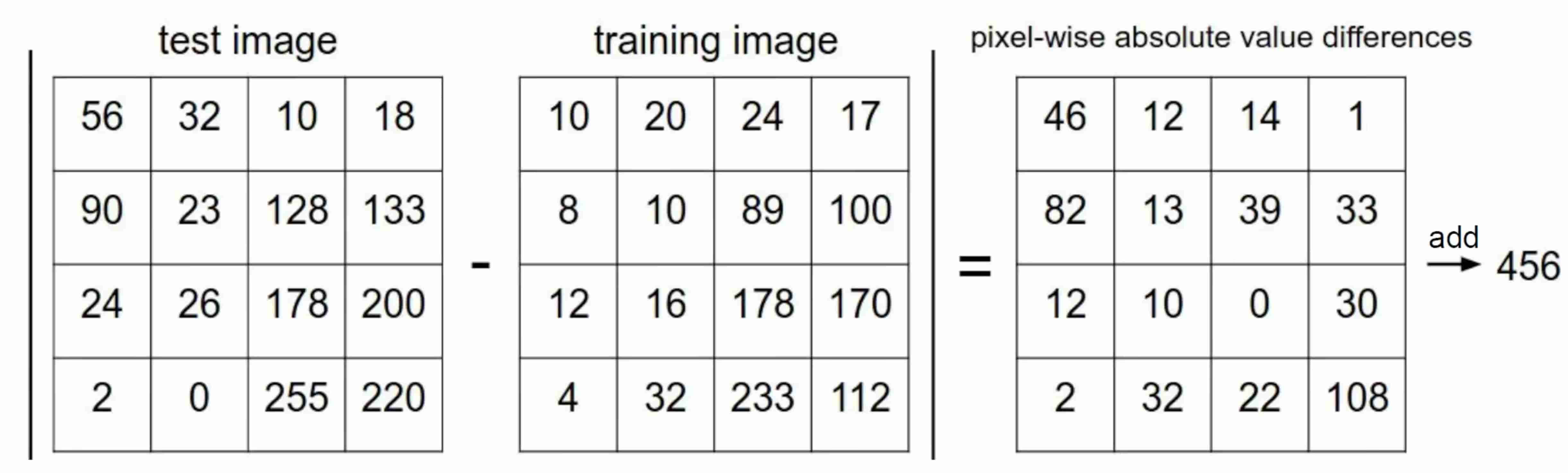也称为曼哈顿距离
import numpy as np
class NearestNeighbor:
def __init__(self):
pass # 空操作不执行任何初始化
def train(self,X,y):
#X是N*D，每行是一个样本
self.Xtr=X#存储数据
self.ytr=y#存储标签
def predict(self,X):
num_test=X.shape[0]
Ypred=np.zeros(num_test,dtype=self.ytr.dtype)
for i in range(num_test):
distances=np.sum(np.abs(self.Xtr-X[i,:]),axis=1)#求和曼哈顿距离
min_index=np.argmin(distances)
Ypred[i]=self.ytr[min_index]
return Ypred
- X.shape获得数据数量=（行数，列数）——>X.shape[0]即是行数，而每行是一个样本，所以获取的是样本数量。
- zeros用来创建初始值都为0的数组
- abs是绝对值
- argmin返回第一个最小值索引
#最近邻决策边界
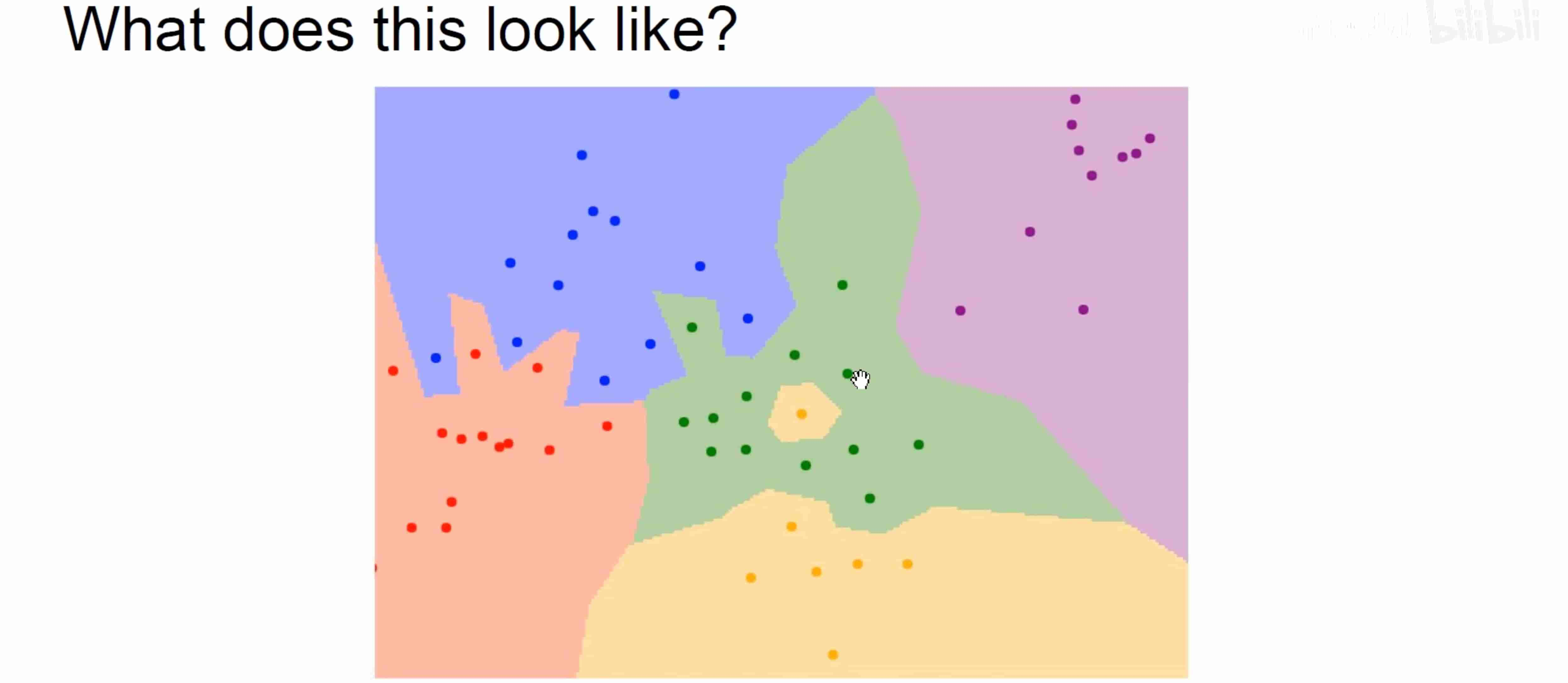边界线是各个异色点的垂直平分线（即对于两色点之间 在边界线的哪一侧，就是距离哪个更接近一点。此种情况只考虑两个点
然而这幅图中边界线有很多棱角，这说明读取到了噪声点
为了提升泛化能力——>k最近邻算法%%考虑邻近的k个点，类似投票表决
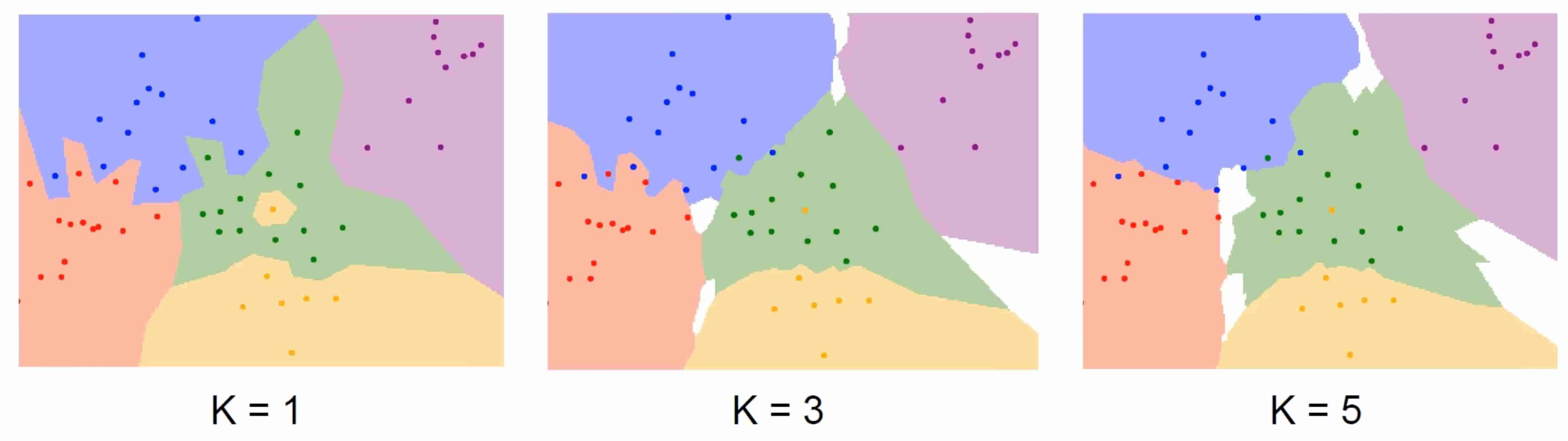但是k的值并不是越大越好！ 否则图上的所有点都会变成同个类别
除了$L_1$曼哈顿距离，还有$L_2$ （欧氏距离、欧几里得）$d_2 (I_1,I_2)=\sqrt{\sum\limits_{p}(I_1^p-I_2^p)^2}$
def compute_distances_two_loops(self, X_test):
num_test = X_test.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train)) # 初始化距离矩阵
for i in range(num_test):
for j in range(num_train):
# 计算 L2 距离（欧氏距离）
dists[i, j] = np.sqrt(np.sum((X_test[i] - self.X_train[j]) ** 2))
return dists
超参数（hyperparameters）
- k的值
- 采用哪种距离（$L_1 or L_2$）
如何设置超参数
- 选择在数据集中表现最佳的超参数（把整个数据集当成训练集） 缺点：k=1在训练集中一直都表现良好
- 将数据集封城了训练集和测试集两部分 缺点：对于算法在新数据表现如何无法得知
- 将数据集分为训练集、验证集和测试集然后再验证集中选取合适的超参数，并在测试集进行验证 最佳方法！
- 将数据集分成好几个folds，每次用不同的fold作为验证集 #交叉验证 缺点：只适合用于数据集规模较小的时候，在深度学习中不常用 优点：可以尽可能避免偶然性
线性分类器
代数角度
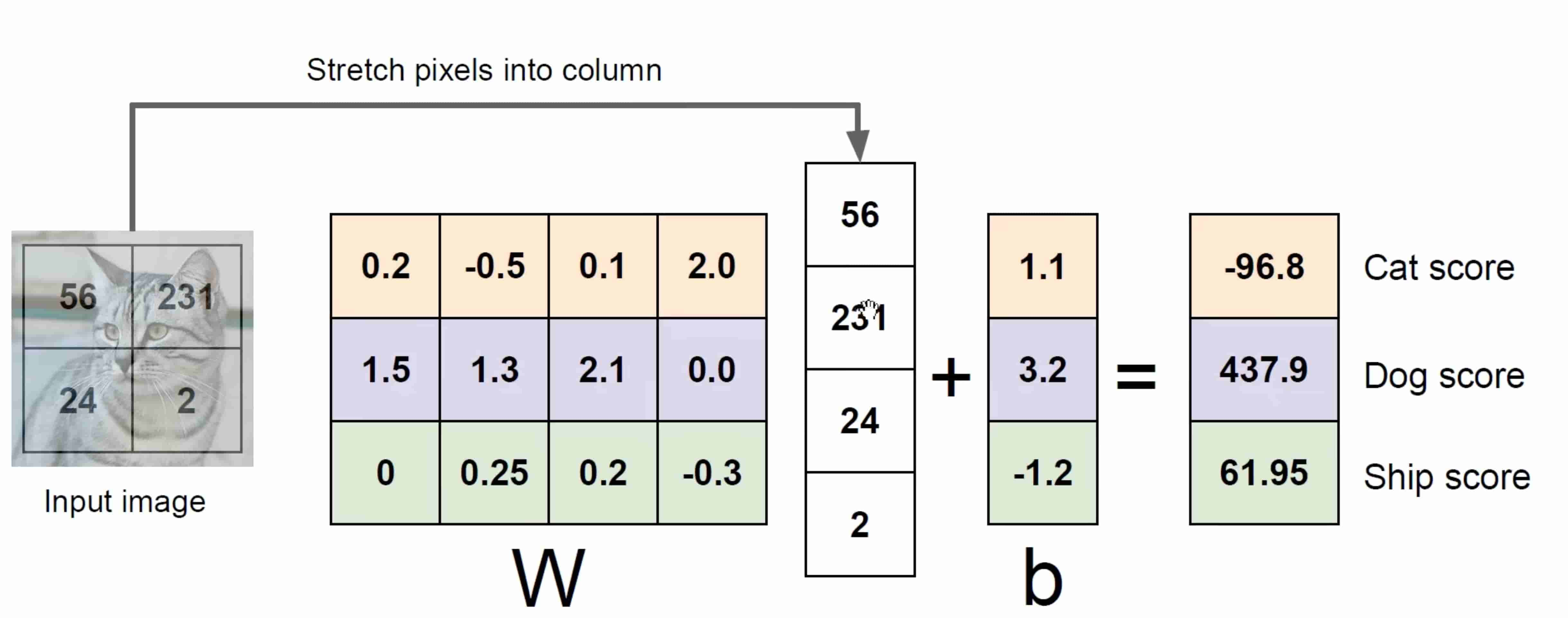
矩阵相乘（W是个矩阵） 本质：对应像素位置* 对应像素权重+对应截距
视觉角度
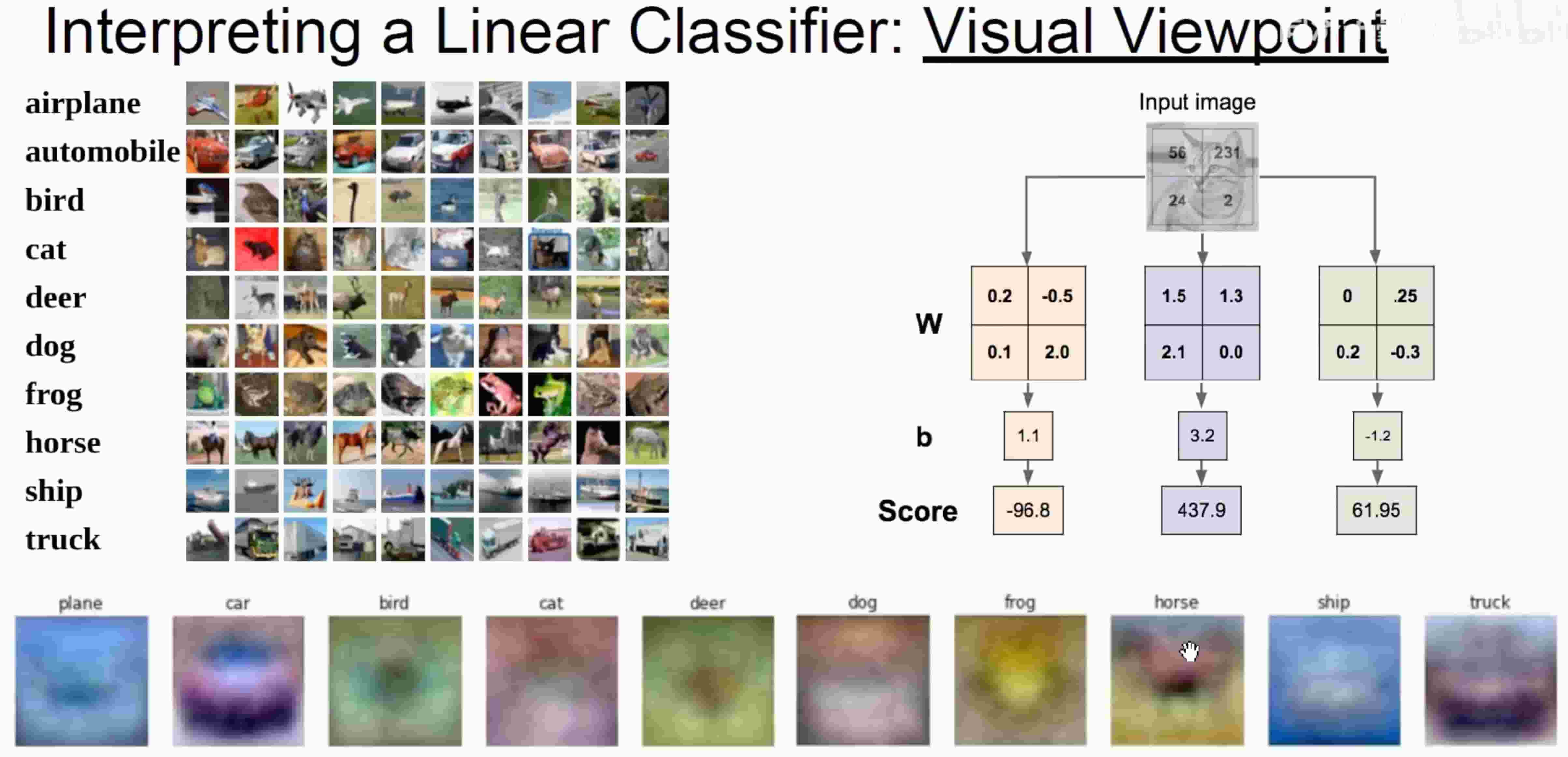
观察像素块的占比权重（eg：如果图像中央存在大量绿色 会更偏向识别成青蛙
几何角度
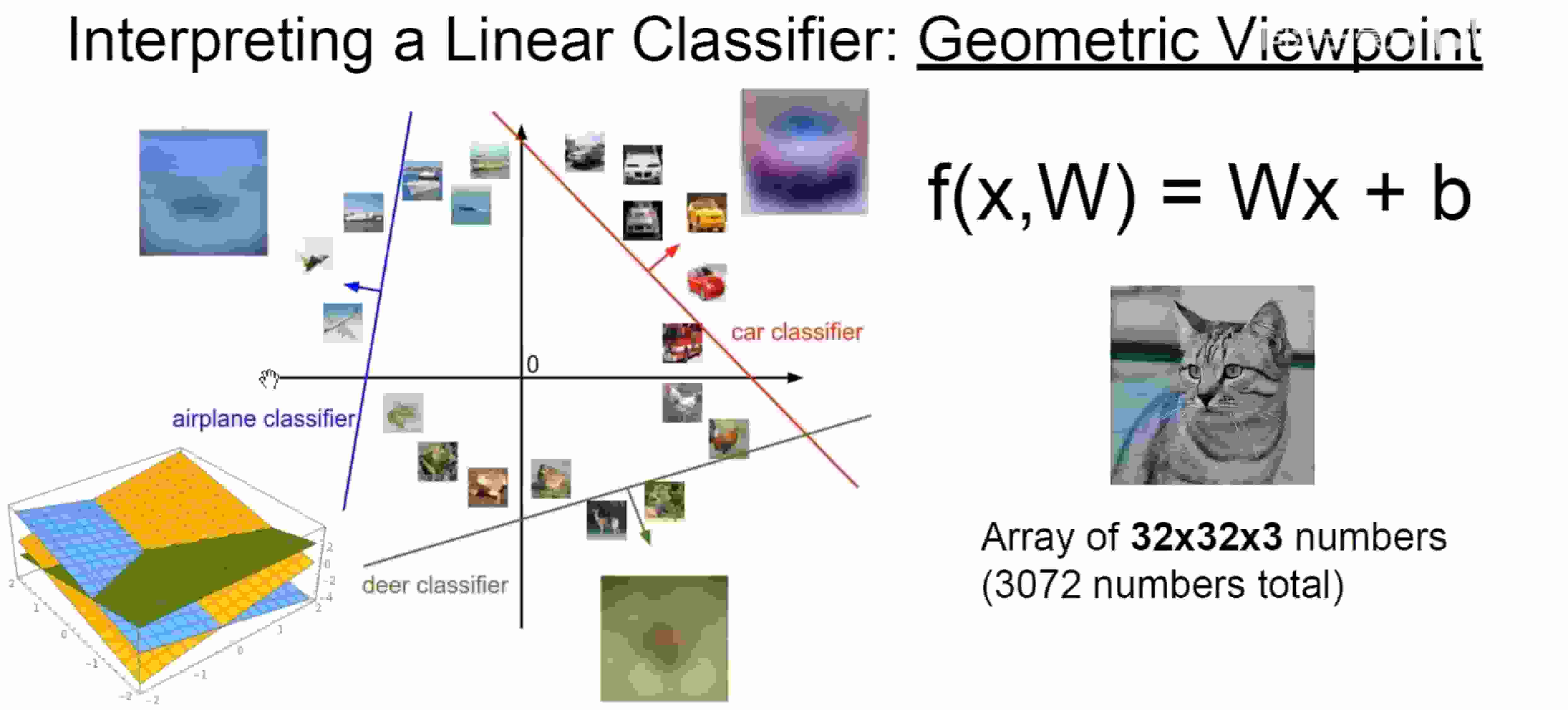
线性分类器可以看作是空间的分界
- 一维空间是一个点
- 二维空间是一条直线
- 三维空间是一个平面
- 多维空间是复杂曲面……
